Procesos aleatorios

Los procesos aleatorios son los terceros “objetos aleatorios” por analizar. Incorporan una segunda variable independiente, el tiempo, que los hace útiles en la descripción de fenómenos cambiantes o dinámicos tales como las señales y los sistemas.

WARNING

Transcripción faltante de 4_13_1_concepto_estocastico.md

---

Clasificación de procesos

WARNING

Se deben cambiar las imágenes 13_variaciones_aleatorias.png y 13_secuencia_aleatoria.png por el svg correspondiente debido a que no se adjuntó en la carpeta /img.

Definición de una variable aleatoria

• Proceso aleatorio continuo El caso si $X$ es un proceso continuo y $t$ toma un continuo de valores.

• Proceso aleatorio discreto Corresponde a la variable aleatoria $X$ que toma solamente valores discretos mientras que $t$ es continuo.

• Secuencia aleatoria continua Un proceso aleatorio para el que $X$ es continuo pero el tiempo tiene solamente valores discretos (al muestrear periódicamente los miembros del agregado de un proceso aleatorio continuo).

• Secuencia aleatoria discreta Corresponde al caso de variables aleatorias discretas y tiempo discreto.

	Valores continuos	Valores discretos
Tiempo continuo	Proceso aleatorio continuo	Proceso aleatorio discreto
Tiempo discreto	Secuencia aleatoria continua	Secuencia aleatoria discreta

Ejemplo de una secuencia aleatoria continua

A continuación, se presenta una representación gráfica de una secuencia aleatoria continua.

Procesos determinísticos y no determinísticos

Un proceso aleatorio puede describirse por la forma de sus funciones muestra.

• Si valores futuros de cualquier función muestra no pueden ser predichos exactamente de valores observados pasados, el proceso se denomina no determinístico.

• Un proceso se llama determinístico si los valores futuros de cualquier función muestra pueden ser predichos de valores pasados.

Ejemplo de proceso aleatorio determinístico con función exponencial

Sea un proceso aleatorio definido por:

$$X(t)=A{e}^{-t}u(t)$$

donde $A$ es una variable aleatoria discreta que puede tomar los valores $\{1,2,3\}$ con igual probabilidad.

---

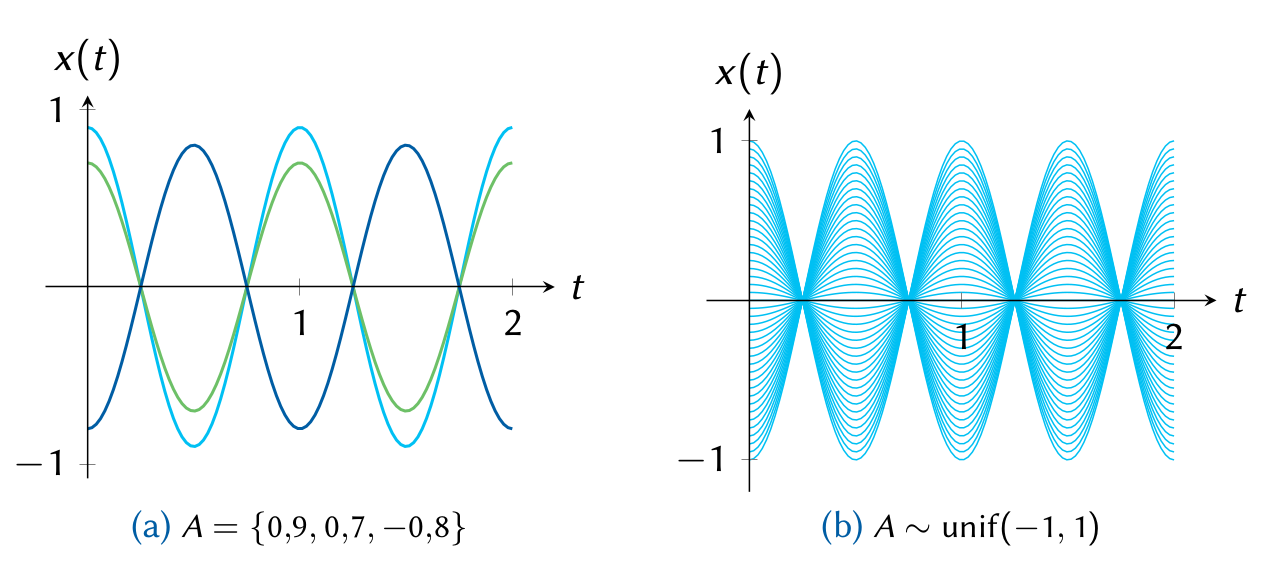
Ejemplo de variaciones en la amplitud para una onda sinusoidal

Una señal tiene la forma deseada:

$$v(t)=v_0+a\cos ({\omega }_{0}t+{\theta }_0)$$

pero su recepción puede estar seriamente afectada por un canal de transmisión que agrega ruido, inflexiones de onda, reverberaciones, etc. Se puede por ahora asumir que existen únicamente variaciones aleatorias en la amplitud, modeladas como un proceso aleatorio:

$$X(t)=v_0+A\cos ({\omega }_{0}t+{\theta }_0)$$

donde $A\sim \mathsf{unif}(-1,1)$.

Para $A\sim \mathsf{unif}(-1,1)$, $v_0=0$, ${\omega }_0=2\pi$ y ${\theta }_0=0$ se tiene la siguiente representación gráfica:

:::

Función general para variaciones en la amplitud

En general, para una función de la forma:

$$X(t)=A\cos ({\omega }_{0}t+\mathrm{\Theta })$$

$A$, $\mathrm{\Theta }$ u ${\omega }_0$ (o todos) pueden ser variables aleatorias. Cualquier función muestra corresponde a la ecuación anterior con valores particulares de estas variables aleatorias.

• Si se conoce la función muestra en un instante del tiempo, se puede predecir su comportamiento futuro, dado que la forma es conocida y, por lo tanto, determinística.

Funciones de distribución de un proceso aleatorio

WARNING

Existen algunos errores en la transcripción de 4_13_4_estacionaridad.md

Función de probabilidad acumulativa de primer orden

Para un tiempo particular $t_1$, la función de probabilidad acumulativa asociada con la variable aleatoria $X_1=X(t_1)$, será denotada $F_X(x_1;t_1)$ y es conocida más precisamente como la función acumulativa de primer orden del proceso $X(t)$. Se le define como

$$F_X(x_1;t_1)=P(X(t_1)\le x_1)$$

para cualquier número real $x_1$.

Función de probabilidad acumulativa de segundo orden

Para dos variables aleatorias $X_1=X(t_1)$ y $X_2=X(t_2)$, la función acumulativa conjunta de segundo orden es la extensión bidimensional de la fórmula anterior:

$$F_X(x_1,x_2;t_1,t_2)=P\{X(t_1)\le x_1,X(t_2)\le x_2\}$$

De manera similar, para $N$ variables aleatorias $X_i=X(t_i),i=1,2,\dots ,N$, la función acumulativa conjunta de orden $N$ es

$$F_X(x_1,\dots ,x_N;t_1,\dots ,t_N)=P\{X(t_1)\le x_1,\dots ,X(t_N)\le x_N\}$$

Funciones de densidad de probabilidad

Las funciones de densidad conjunta de interés se encuentran de las derivadas apropiadas de las tres fórmulas anteriores:

$$\begin{array}{rl}{f}_X(x_1;t_1)& =\frac{\partial }{\partial x_1}{F}_X(x_1;t_1)\\ f_X(x_1,x_2;t_1,t_2)& =\frac{{\partial }^2{F}_X(x_1,x_2;t_1,t_2)}{\partial x_1\partial x_2}\\ f_X(x_1,\dots ,x_N;t_1,\dots ,t_N)& =\frac{{\partial }^N{F}_X(x_1,\dots ,x_N;t_1,\dots ,t_N)}{\partial x_1\cdots \partial x_N}\end{array}$$

:::

Función de densidad de un proceso on función exponencial

Problema:
¿Cuál es la función de densidad para este proceso aleatorio?

$$X(t)=A{e}^{-t}u(t)$$

donde $A$ es una variable aleatoria discreta que puede tomar los valores $\{1,2,3\}$ con igual probabilidad.

Solución:
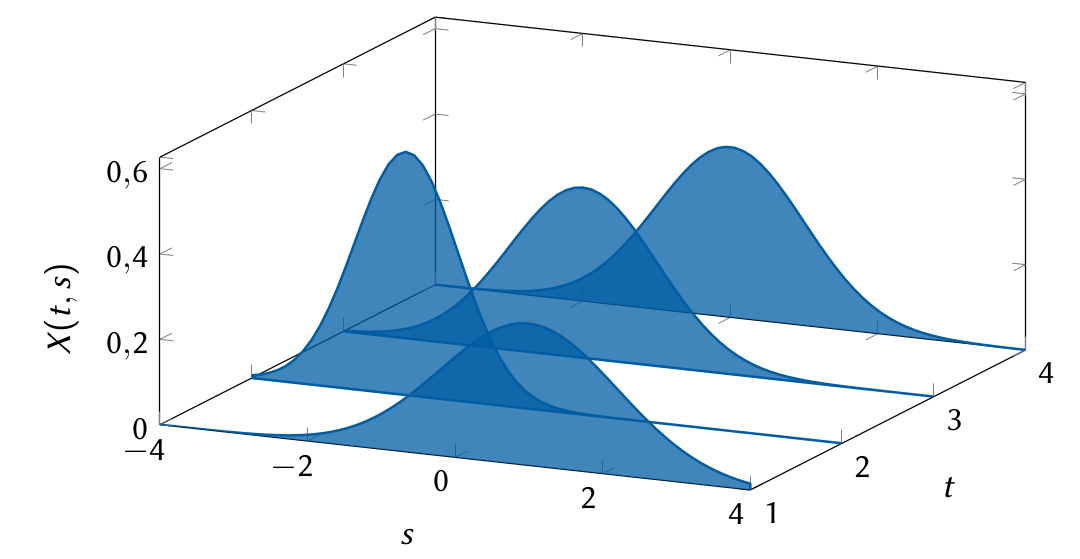
La función de densidad probabilística $f_X(x,t)$ puede deducirse analizando que:

• En $t=1$ el proceso aleatorio $X(1)$ puede tomar los valores $e^{-1}$, $2e^{-1}$ o $3e^{-1}$, cada uno con probabilidad $\frac{1}{3}$, por tanto:

$$f_X(x,1)=\frac{1}{3}\delta (x-e^{-1})+\frac{1}{3}\delta (x-2e^{-1})+\frac{1}{3}\delta (x-3e^{-1})$$

• Esto se puede generalizar para cualquier $t$ como:

$$f_X(x,t)=\frac{1}{3}\delta (x-e^{-t})+\frac{1}{3}\delta (x-2e^{-t})+\frac{1}{3}\delta (x-3e^{-t})$$

La función de densidad es una secuencia de funciones definidas para cada instante de tiempo (discreto o continuo).

• Para la función de densidad conjunta en dos tiempos $t_1$ y $t_2$:

$$\begin{array}{rl}{f}_X(x_1,x_2,t_1,t_2)=& \frac{1}{3}\delta (x_1-e^{-t_1},x_2-e^{-t_2})\\ & +\frac{1}{3}\delta (x_1-2e^{-t_1},x_2-2e^{-t_2})\\ & +\frac{1}{3}\delta (x_1-3e^{-t_1},x_2-3e^{-t_2})\end{array}$$

Conclusión:
La función de densidad para cualquier tiempo $t$ es:

$$f_X(x,t)=\frac{1}{3}\delta (x-e^{-t})+\frac{1}{3}\delta (x-2e^{-t})+\frac{1}{3}\delta (x-3e^{-t})$$

---

Independencia estadística

Independencia estadística

Dos procesos $X(t)$ e $Y(t)$ son estadísticamente independientes si para cualquier elección de tiempos:

$$t_1,t_2,\dots ,t_N\text{y}{t}_1^{\prime },t_2^{\prime },\dots ,t_M^{\prime }$$

el grupo de variables aleatorias $X(t_1),\dots ,X(t_N)$ es independiente del grupo $Y(t_1^{\prime }),\dots ,Y(t_M^{\prime })$. Esto requiere que:

$$\begin{array}{rl}& f_{X,Y}(x_1,\dots ,x_N,y_1,\dots ,y_M;t_1,\dots ,t_N,t_1^{\prime },\dots ,t_M^{\prime })=\\ & f_X(x_1,\dots ,x_N;t_1,\dots ,t_N)\cdot f_Y(y_1,\dots ,y_M;t_1^{\prime },\dots ,t_M^{\prime })\end{array}$$